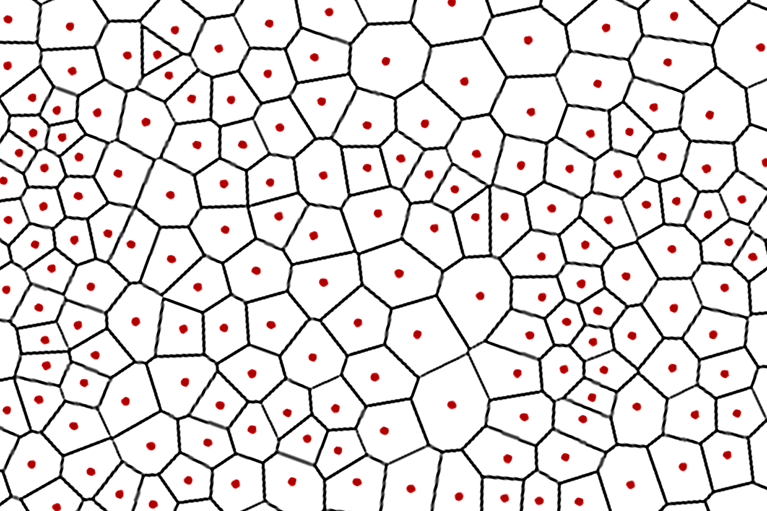
The Voronoi diagram for a finite set of N points on a plane (which in our case are pore centers) shows a partition of the plane in such a way that each region of this partition forms a set of points which are closer to one of the elements of the N set than to any other element of this set. The regions formed after partitioning are convex polygons, and the number of vertices of each separately taken polygon is equal to the number of neighbours of the pore located inside it.
The construction of the distribution by the number of neighbours can be performed using Statistics2D software (developer: Dmitry S. Koshkodaev). The input data are the coordinates of the centres of mass of each pore in the analyzed image. With the help of the obtained information, it is possible to determine the fraction of pores in a hexagonal coordination, a parameter by which one can quantitatively compare the degree of ordering of the porous structure of the samples obtained under different anodizing conditions (see Fig. 1).
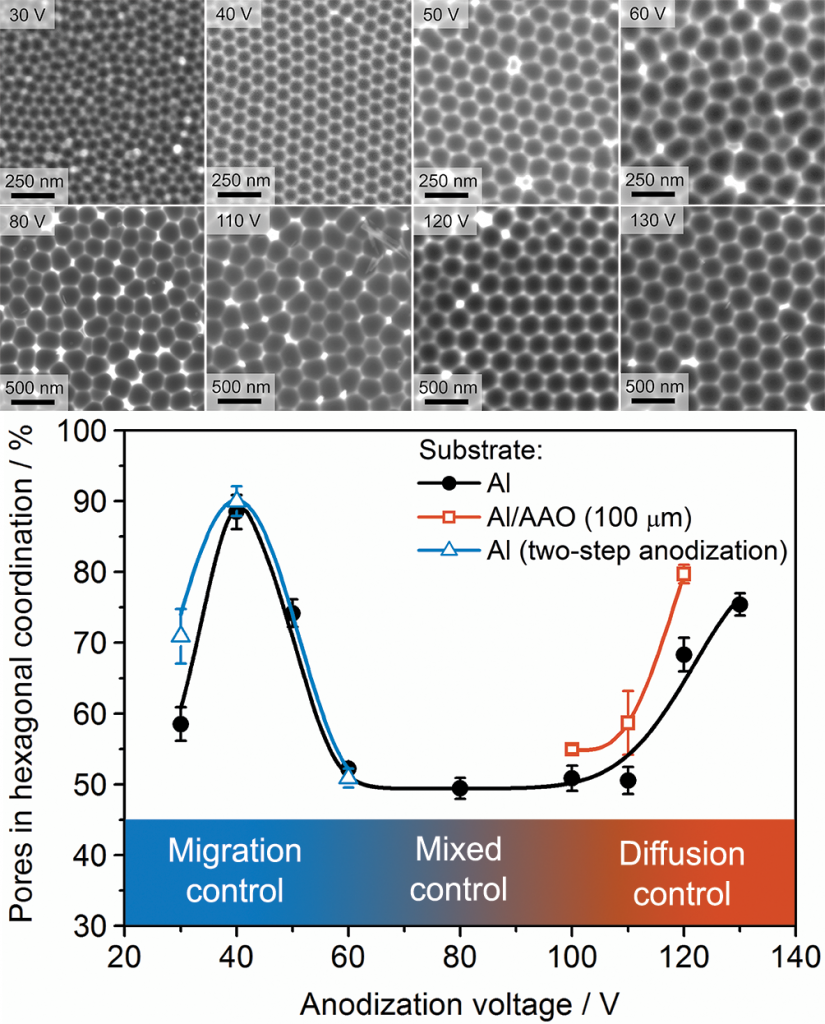
Figure 1. SEM images of the surface of aluminium replicas obtained after dissolving anodic aluminium oxide films formed at different voltages in 0.3 M H2C2O4 (top). The fraction of pores in hexagonal coordination, calculated using the Statistics2D software based on several SEM micrographs containing more than 105 pores [I.V. Roslyakov, E.O. Gordeeva, K.S. Napolskii, Role of Electrode Reaction Kinetics in Self-Ordering of Porous Anodic Alumina // Electrochimica Acta, 2017, v. 241, pp. 362–369].
For free download of the Statistics2D software and the instruction on its application for calculating the number of neighbours of each pore, please, follow the link below.
Using the information extracted from the Voronoi diagram for the porous structure of anodic alumina, one can calculate a local ordering parameter (ψ), which simultaneously characterizes the orientation and positional ordering [J.R. Borba et al., Quantitative Characterization of Hexagonal Packings in Nanoporous Alumina Arrays: A Case Study // The Journal of Physical Chemistry C, 2012, v. 117(1), pp. 246–251]. The ψ parameter can be calculated by the formula:
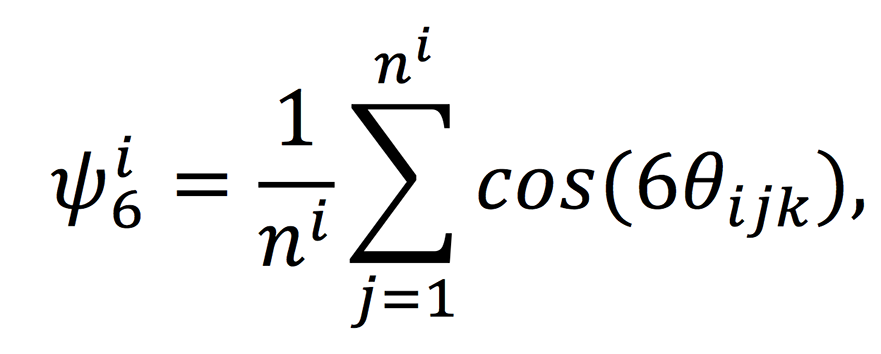
where θijk is the angle between 3 adjacent pores, ni s the number of neighbours around the ith pore. Note that for an ideal hexagonal packing <ψ> = 1, and for an absolutely disordered structure <ψ> = 0. This parameter can also be calculated using Statistics2D software.
If you used our program and found it useful, please, cite our work [I.V. Roslyakov, D.S. Koshkodaev, A.A. Eliseev, D. Hermida-Merino, V.K. Ivanov, A.V. Petukhov, K.S. Napolskii. Growth of Porous Anodic Alumina on Low-Index Surfaces of Al Single Crystals // The Journal of Physical Chemistry C, 2017. DOI: 10.1021/acs.jpcc.7b09998] in your scientific papers.